Reliability in Education Research: A Deeper Examination

Presented by Joe Tise, PhD, Senior Education Researcher at IACE

We can view reliability in education research as inherently linked to measurement error. For example, to be confident in claims we make about something we assess, the assessment must produce reliable data. A thermometer that says it’s 72 degrees Fahrenheit one minute, but 56 degrees the next would not instill confidence. Likewise, a measure of a student’s computational thinking skills that places the student in the top 1% of all students one day, but the next places them in the bottom 5% would not be very useful. Clearly, any measure that produces data with that much variation likely contains a lot of error in the measurement (assuming no true change in the measured variable occurred).

The Standards for Educational and Psychological Testing defines reliability as “the more general notion of consistency of the scores across instances of the testing procedure” (American Educational Research Association et al., 2014, p. 33). Note in this definition that reliability refers to the data, not the test itself. Tests that produce data that are not reliable contain more error than tests that produce highly reliable data.

In a never-ending quest for enhanced approaches to measuring latent (i.e., unobserved) constructs, psychometricians have developed three major theories of assessment over the last century: Classical Test Theory (CTT), Generalizability Theory (G Theory), and Item-response Theory (IRT). Each of these frameworks seeks to minimize error and therefore enhance data reliability. They differ, however, in their approach.

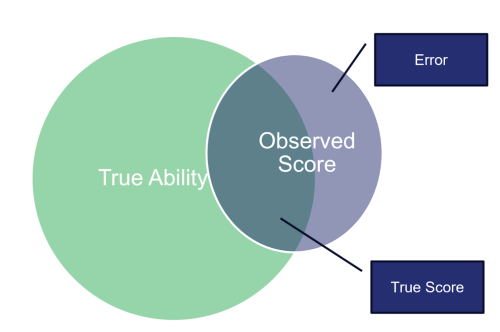
CTT (Traub, 1997) conceptualizes error as a unitary latent construct: any part of an observed test score that is not a participant’s true score is considered error. CTT provides no way to further decompose error, which is why G Theory was developed shortly after. G Theory (Brennan, 2001) provides researchers the ability to determine how much of an observed score is attributable to different sources of error, such as the occasion of measurement or the item format. To accomplish this, a researcher must first define two things: the universe of admissible observations and the universe of generalization. IRT (Hambleton et al., 1991; Hambleton & Swaminathan, 1985) works from a slightly different perspective. CTT and G Theory consider the test as a whole, but as its name suggests, IRT focuses more specifically on individual items. Thus, from an IRT perspective, reliable data is produced from items that can effectively differentiate lower from higher performers. An item’s ability to differentiate participants by ability level directly impacts the amount of information provided by that item, and item information gives the researcher a sense of the item’s quality (i.e., higher item information means higher item quality).

This blog post is far too short to sufficiently describe these three theories of assessment in any detail, but I suggest that interested readers explore the references section for more detailed overviews of each theory. Even a basic understanding of these assessment theories can help researchers design better measures and evaluate the quality of existing measures. To the extent we can reduce error in measurement, we can simultaneously enhance reliability in education research.

References

American Educational Research Association, American Psychological Association, & National Council on Measurement in Education. (2014). Standards for Educational and Psychological Testing. American Educational Research Association.

Brennan, R. L. (2001). Generalizability Theory. Springer-Verlag Berlin Heidelberg. https://doi.org/10.1007/978-1-4757-3456-0

Hambleton, R. K., & Swaminathan, H. (1985). Item Response Theory: Principles and Applications. Springer Science+Business Media.

Hambleton, R. K., Swaminathan, H., & Rogers, H. J. (1991). Fundamentals of Item Response Theory. Sage Publications, Inc.
Traub, R. E. (1997). Classical Test Theory in historical perspective. Educational Measurement: Issues and Practice, 8–14.