Archive: 2024
Validity and Reliability in Qualitative Research
Comments Off on Validity and Reliability in Qualitative ResearchPost prepared and written by Joe Tise, PhD, Senior Education Researcher
In this series we have discovered the many ways in which evidence of validity can be produced and ways in which reliable data can be produced. To be sure, the bulk of this series was focused on quantitative research, but any mixed-methods or qualitative researcher will tell you that quantitative research only tells us one piece of the puzzle.
Qualitative research is needed to answer questions not suited for quantitative research, and validity and reliability need to be considered in qualitative research too. Qualitative research includes numerous methodological approaches, such as individual and focus group interviews, naturalistic observations, artifact analysis, and even open-ended survey questions. Unlike quantitative research–which utilizes forms, surveys, tests, institutional data, etc.–in qualitative research, the researcher often is the data collection mechanism and the analysis mechanism.
Researchers usually don’t run a statistical analysis on qualitative data; instead, a researcher typically analyzes the qualitative data, extracts meaning from it, and answers a research question from that meaning. Though this is similar to quantitative research, some of the analysis methods can be viewed as more subjective.
So, how can we know that results obtained from a qualitative analysis reflect some truth, and not the researcher’s personal biases, experiences, or lenses?
Reliability and validity are equally important to consider in qualitative research. Ways to enhance validity in qualitative research include:
- Use multiple analysts
- Create/maintain audit trails
- Conduct member checks
- Include positionality statements
- Solicit peer review of analytical approach
- Triangulate findings via multiple data sources
- Search for and discuss negative cases (i.e., those which refute a theme)
Building reliability can include one or more of the following:
- Clearly define your codes and criteria for applying them
- Use detailed transcriptions which include things like pauses, crosstalk, and non-word verbal expressions
- Train coders on a common set of data
- Ensure coders are consistent with each other before coding the reset of the data
- Periodically reassess interrater agreement/reliability
- Use high-quality recording devices
The most well-known measure of qualitative reliability in education research is inter-rater reliability and consensus coding. I want to make a distinction between two common measures of inter-rater reliability: percent agreement and Cohen’s Kappa.
Percent agreement refers to the percentage of coding instances in which two raters assign the same code to a common “piece” of data. Because this is a simple percentage, it’s more intuitive to understand. But it also does not account for chance–in any deductive coding framework (i.e., when all possible codes are already defined), there is a random chance that two coders will apply the same code without actually “seeing” the same thing in the data.
By contrast, Cohen’s Kappa is designed to parse out the influence of chance agreement, and for this reason Cohen’s Kappa will always be smaller than the percent agreement for a given dataset. Many qualitative data analysis software packages (e.g., NVivo) will calculate both percent agreement and Cohen’s Kappa.
In consensus coding, multiple raters code the same data, discuss the codes that may apply, and decide together how to code the data. With consensus coding, the need for inter-rater agreement/reliability metrics is circumvented, because by definition, you will always have 100% agreement/reliability. The major downside of consensus coding is, of course, the time and effort needed to engage it. With large sets of qualitative data, consensus coding may not be feasible.
For a deeper dive into these topics, there are many excellent textbooks that explore the nuances of qualitative validity and reliability. Below, you’ll find a selection of recommended resources, as well as others that provide detailed insights into strengthening qualitative research methods.
Resources
Corbin, J., & Strauss, A. (2015). Basics of Qualitative Research: Techniques and Procedures for Developing Grounded Theory (4th ed.). Sage Publications.
Creswell, J. W., & Báez, J. C. (2021). 30 Essential Skills for the Qualitative Researcher (2nd ed.). Sage Publications.
Creswell, J. W., & Poth, C. N. (2018). Qualitative inquiry and research design: Choosing among five approaches. Sage Publications.
Saldaña, J. (2013). An introduction to codes and coding. In The coding manual for qualitative researchers (pp. 1–40). Sage Publications.
Reliability in Education Research: A Deeper Examination
Comments Off on Reliability in Education Research: A Deeper ExaminationPresented by Joe Tise, PhD, Senior Education Researcher at IACE
We can view reliability in education research as inherently linked to measurement error. For example, to be confident in claims we make about something we assess, the assessment must produce reliable data. A thermometer that says it’s 72 degrees Fahrenheit one minute, but 56 degrees the next would not instill confidence. Likewise, a measure of a student’s computational thinking skills that places the student in the top 1% of all students one day, but the next places them in the bottom 5% would not be very useful. Clearly, any measure that produces data with that much variation likely contains a lot of error in the measurement (assuming no true change in the measured variable occurred).
The Standards for Educational and Psychological Testing defines reliability as “the more general notion of consistency of the scores across instances of the testing procedure” (American Educational Research Association et al., 2014, p. 33). Note in this definition that reliability refers to the data, not the test itself. Tests that produce data that are not reliable contain more error than tests that produce highly reliable data.
In a never-ending quest for enhanced approaches to measuring latent (i.e., unobserved) constructs, psychometricians have developed three major theories of assessment over the last century: Classical Test Theory (CTT), Generalizability Theory (G Theory), and Item-response Theory (IRT). Each of these frameworks seeks to minimize error and therefore enhance data reliability. They differ, however, in their approach.
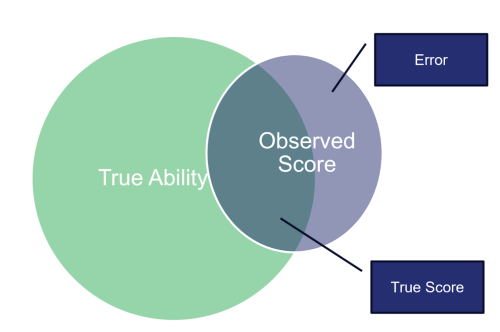
CTT (Traub, 1997) conceptualizes error as a unitary latent construct: any part of an observed test score that is not a participant’s true score is considered error. CTT provides no way to further decompose error, which is why G Theory was developed shortly after. G Theory (Brennan, 2001) provides researchers the ability to determine how much of an observed score is attributable to different sources of error, such as the occasion of measurement or the item format. To accomplish this, a researcher must first define two things: the universe of admissible observations and the universe of generalization. IRT (Hambleton et al., 1991; Hambleton & Swaminathan, 1985) works from a slightly different perspective. CTT and G Theory consider the test as a whole, but as its name suggests, IRT focuses more specifically on individual items. Thus, from an IRT perspective, reliable data is produced from items that can effectively differentiate lower from higher performers. An item’s ability to differentiate participants by ability level directly impacts the amount of information provided by that item, and item information gives the researcher a sense of the item’s quality (i.e., higher item information means higher item quality).
This blog post is far too short to sufficiently describe these three theories of assessment in any detail, but I suggest that interested readers explore the references section for more detailed overviews of each theory. Even a basic understanding of these assessment theories can help researchers design better measures and evaluate the quality of existing measures. To the extent we can reduce error in measurement, we can simultaneously enhance reliability in education research.
References
American Educational Research Association, American Psychological Association, & National Council on Measurement in Education. (2014). Standards for Educational and Psychological Testing. American Educational Research Association.
Brennan, R. L. (2001). Generalizability Theory. Springer-Verlag Berlin Heidelberg. https://doi.org/10.1007/978-1-4757-3456-0
Hambleton, R. K., & Swaminathan, H. (1985). Item Response Theory: Principles and Applications. Springer Science+Business Media.
Hambleton, R. K., Swaminathan, H., & Rogers, H. J. (1991). Fundamentals of Item Response Theory. Sage Publications, Inc.
Traub, R. E. (1997). Classical Test Theory in historical perspective. Educational Measurement: Issues and Practice, 8–14.
Validity in Educational Research: A Deeper Examination
Comments Off on Validity in Educational Research: A Deeper ExaminationPresented by Joe Tise, PhD, Senior Education Researcher at IACE
The concept of validity, including validity of educational research, has evolved over millennia. Some of the earliest examples of how validity influenced society at scale comes from the ancient Chinese Civil Service exam programs (Suen & Yu, 2006). Back in 195 BCE, Emperor Liu Bang decreed that men of virtue and ability ought to serve the nation in various capacities. With that decree, Emperor Bang established the “target” for assessment against which the effectiveness of various assessments would be judged. Assessments which could more readily select men of virtue and ability would be considered more useful than those which could not. Over the next 2,000 years, the Chinese Civil Service exam took many forms: expert observational ratings, writing poetry, drafting philosophical essays, and portfolio submissions, among other variations.
The concept of validity has been deliberated in Western cultures as well since at least the early 1900s. Early conceptions viewed validity merely as a statistical coefficient, such that even a correlation coefficient could measure validity (Bingham, 1937; Hull, 1928). You need only to examine the numerous spurious correlations demonstrated by Tyler Vigen to see that a simple correlation cannot sufficiently capture the true nature of validity. Fortunately, this reductive view of validity did not persist long–it was soon overtaken by an ancestor of present validity conceptions. By the 1950s, psychometricians detailed multiple “types” of validity, such as predictive, concurrent, construct, and content validity (American Psychological Association, 1954).
Still, this conception of validity misinterpreted the unitary nature of validity. Philosophical deliberations largely concluded in 1985 when the Joint Committee for the Revision of the Standards for Educational and Psychological Testing (Joint Committee; comprised of the APA, AERA, and NCME) established validity as one unitary construct that does not have multiple “types” but rather multiple sources of validity evidence (American Educational Research Association et al., 1985). In 2014, the Joint Committee further clarified that validity refers to the “the degree to which evidence and theory support the interpretations of test scores for proposed uses of tests” (American Educational Research Association et al., 2014). Thus, “validity” applies to our interpretations and uses of tests, not the test itself.
The contemporary view of validity details five primary sources of validity evidence, presented in the table below (in no particular order).
| Source of Validity Evidence | Description | Example of How to Assess |
|---|---|---|
| Test content | Themes, wording, and format of the items, tasks, or questions on a test | Expert judgment; delphi method; content specifications |
| Response processes | The extent to which test takers actually engage the cognitive/behavioral processes the test intends to assess | Analyze individual test responses via interviews; examine early drafts of a response (e.g., written response or math problem); eye-tracking |
| Test structure | The degree to which the relationships among test items and test components conform to the construct on which the proposed test score interpretations are based | Exploratory factor analysis; confirmatory factor analysis; differential item functioning analysis |
| Relations to other variables | Do scores on the test relate in the expected way to other variables and/or other tests of the same construct? | Correlate test scores with other variables; regress test scores on other variables |
| Test consequences | Must evaluate the acceptability of (un)intended consequences from interpretations and uses of the test scores | Does the test incentivize cheating? Are certain subgroups systematically harmed by the test? |
I will note here that although there are multiple sources of validity evidence, a researcher does not necessarily have to provide evidence from all sources for a given test or measure. Some sources of validity evidence will not be relevant to a test.
For example, evidence of test structure is largely nonsensical for a simple one or two-item “test” of a person’s experience with, say, teaching computer science (e.g., asking someone how many years of experience they have in computer science). Similarly, a measure of someone’s interest in computer science likely does not require evidence based on response processes, because reporting interest in a topic does not really invoke any cognitive or behavioral processes (other than reflection/recall, which is not the target of the test).
References
American Educational Research Association, American Psychological Association, & National Council on Measurement in Education. (1985). Standards for educational and psychological testing. Author.
American Educational Research Association, American Psychological Association, & National Council on Measurement in Education. (2014). Standards for Educational and Psychological Testing. American Educational Research Association.
American Psychological Association. (1954). Technical recommendations for psychological tests and diagnostic techniques. Psychological Bulletin, 51(2), 1–38. https://doi.org/10.1037/h0053479
Bingham, W. V. (1937). Aptitudes and aptitude testing (pp. viii, 390). Harpers.
Hull, C. L. (1928). Aptitude Testing (L. M. Terman, Ed.). World Book Company.https://doi.org/10.1086/498328
Suen, H. K., & Yu, L. (2006). Chronic Consequences of High‐Stakes Testing? Lessons from the Chinese Civil Service Exam. Comparative Education Review, 50(1), 46–65. https://doi.org/10.1086/498328
Demystifying Reliability and Validity in Educational Research
Comments Off on Demystifying Reliability and Validity in Educational ResearchPost prepared and written by Joe Tise, PhD, Senior Education Researcher
In the past, reliability and validity may have been explained to you by way of an analogy: validity refers to how close to the “bullseye” you can get on a dart board, while reliability is how consistently you throw your darts in the same spot (see figure below).
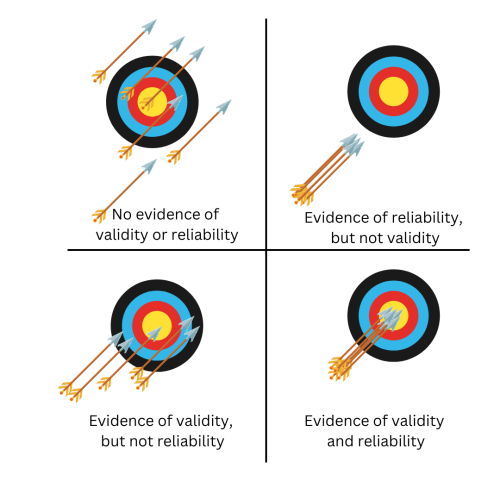
Such an analogy is largely useful, but somewhat reductive. In this four-part blog series, I will dig a bit deeper into validity and reliability to show the different types of each, the different conceptualizations of each, and the relations between them. The structure and content in this blog post comes largely from the Standards for Educational and Psychological Testing (2014), so I highly recommend you get a copy of that book to learn more.
Validity
The Standards (American Educational Research Association et al., 2014) define validity as “the degree to which evidence and theory support the interpretations of test scores for proposed uses of tests.” This definition leads me to make an important distinction at the outset: a test is never valid or invalid—it is the interpretations and uses of that test and decisions made because of a test that are valid or invalid.
To illustrate this point, consider the following scenario. I want to measure students’ reading fluency. I dig into a big pile of data I collected from thousands of K12 students and see that taller students can read longer and more complex books than shorter students. I say to myself:
“Great! To assess new students’ reading fluency, all I need to do is measure how tall they are. Taller students are better readers, after all. Thus, a measure of students’ height must be a valid test of reading fluency.”
Of course, you likely see a problem with my logic. Height may well be correlated with reading fluency (because older children tend to be taller and better readers than younger children), but clearly it is not a test of reading fluency. Nobody would argue that my measuring tape is invalid—just that my use of it to measure reading fluency is invalid. This distinction, obvious as it may seem, is the crux of contemporary conceptions of validity (American Educational Research Association et al., 2014; Kane, 2013). Thus, researchers ought never say a test is valid or invalid but rather, their interpretations or uses of a test are valid or invalid. We may, however, say that an instrument has evidence of validity and reliability while bearing in mind the relevance of such evidence may apply differentially among populations, settings, points in time, or other factors.
Reliability
A similar distinction must be made about reliability—reliability refers to the data, rather than the test itself. A test that produces reliable data will produce the same result for the same participants after multiple administrations, assuming no change in the construct has occurred (e.g., assuming one did not learn more about math between two administrations of the same math test). Thus, The Standards define reliability as “the more general notion of consistency of the scores across instances of the testing procedure.”
But how can you quantify such consistency in the data across testing events? Statisticians have several ways to do this, each differing slightly depending on their theoretical approach to assessment. Each approach utilizes some form of a reliability coefficient, or “the correlation between scores on two equivalent forms of the test, presuming that taking one form has no effect on performance on the second form.” There are many theories of assessment, but three of the most common include Classical Test Theory (Gulliksen, 1950; Guttman, 1945; Kuder & Richardson, 1937), Generalizability Theory (Cronbach et al., 1972; Suen & Lei, 2007; Vispoel et al., 2018) and Item Response Theory (IRT) (Baker, 2001; Hambleton et al., 1991). This blog post is too broad in scope to detail each of these theories, but just know that each theory differs in assumptions made about assessment, terminology used, and each has different implications for how one quantifies data reliability.
What’s Next?
This post only introduces these two terms. The next three posts discuss validity and reliability more in-depth for both quantitative and qualitative approaches (to be published over the next few weeks).
- Validity in Quantitative Education Research: A Deeper Examination
- Reliability in Quantitative Education Research: A Deeper Examination
- Validity and Reliability in Qualitative Education Research
References
American Educational Research Association, American Psychological Association, & National Council on Measurement in Education. (2014). Standards for Educational and Psychological Testing. American Educational Research Association.
Baker, F. B. (2001). The Basics of Item Response Theory (2nd ed.). ERIC Clearinghouse on Assessment and Evaluation. https://eric.ed.gov/?id=ED458219
Cronbach, L. J., Gleser, G. C., Nanda, H., & Rajaratnam, N. (1972). The dependability of behavioral measurements: Theory of generalizability for scores and profiles. John Wiley and Sons.
Gulliksen, H. (1950). Theory of Mental Tests. Wiley.
Guttman, L. (1945). A basis for analyzing test-retest reliability. Psychometrika, 10(4), 255–282. https://doi.org/10.1007/BF02288892
Hambleton, R. K., Swaminathan, H., & Rogers, H. J. (1991). Fundamentals of Item Response Theory. Sage Publications, Inc.
Kane, M. (2013). The argument-based approach to validation. School Psychology Review, 42(4), 448–457. https://doi.org/10.1080/02796015.2013.12087465
Kuder, G. F., & Richardson, M. W. (1937). The theory of the estimation of test reliability. Psychometrika, 2(3), 151–160. https://doi.org/10.1007/BF02288391
Suen, H. K., & Lei, P.-W. (2007). Classical versus Generalizability theory of measurement. Educational Measurement, 4, 1–13.
Vispoel, W. P., Morris, C. A., & Kilinc, M. (2018). Applications of generalizability theory and their relations to classical test theory and structural equation modeling. Psychological Methods, 23(1), 1–26. https://doi.org/10.1037/met0000107
Podcasts! Considering K-5 Computing Education Practices
Comments Off on Podcasts! Considering K-5 Computing Education PracticesWe’re super excited to announce our long-awaited series on K-5 computing education practices!
Our podcasts provide insights from discussions among teachers as they consider meaningful research and how they could adopt new practices into their classrooms.
For educators, these podcasts are meant to provide you with information on various research studies that are may be suitable for your classrooms.
For researchers, the computing education podcasts are meant to insight reflection and further inquiry into how teachers interpret research in context with their classrooms. As we continue our working closing the gap between researchers and practitioners, the discussions can give researchers additional perspectives that they may not already have.
Special thanks to Association of Computing Machinery (ACM) SIGCSE for funding to support the computing education podcasts through a Special Projects grant! We also thank our additional sponsors, Amazon Future Engineer and Siegel Family Endowment, who support our outreach efforts at IACE.
And special thanks to Emily Thomforde for tirelessly leading the discussion groups every week for many years. Shout out to Jordan Williamson (IACE), Emily Nelson (IACE), and Monica McGill (IACE) for creating, modifying, and reviewing the podcasts and briefs!
Either way, we hope you enjoy the podcasts!
- Series opening – Podcast
- K-5 Computing: Design in Action (Abstraction) – Podcast, Practice brief
- Making Computing Meaningful to All Students – Podcast, Practice brief
- Integrating Computing into Literacy and Math – Podcast, Practice brief
- Parsing Parsons Problems for Teaching K-5 Computer Science – Podcast, Practice brief
- Integrating CS into Other Subjects – Podcast, Practice brief
- Physical Computing for K-5 Students – Podcast, Practice brief
- Series closing – Podcast
Join Us at the 2024 ACM SIGCSE Technical Symposium
Comments Off on Join Us at the 2024 ACM SIGCSE Technical SymposiumWe’re always excited to attend the ACM SIGCSE Technical Symposium, and this year is no exception!
You can catch IACE team members (Laycee Thigpen, Joe Tise, Julie Smith, and Monica McGill) at the following events. (Pre-symposium events are invitation only.)
For all the rest, please stop by and say Hi! We’d love to hear about research you’re engaged in that supports learning for all students!
| Day/Time | Event | Authors/Presenters | Location |
|---|---|---|---|
| Tuesday, All day | Reimagining CS Pathways (Invitation only) | Bryan Twarek and Jake Karossel (CSTA), Julie Smith and Monica McGill (IACE) | Off-site |
| Wednesday, All day | Reimagining CS Pathways (Invitation only) | Bryan Twarek and Jake Karossel (CSTA), Julie Smith and Monica McGill (IACE) | Off-site |
| Wednesday, 1-5pm PST | Conducting High-quality Education Research in Computing Designed to Support CS for All (Invitation only) | Monica McGill, Institute for Advancing Computing Education Jennifer Rosato, Northern Lights Collaborative Leigh Ann DeLyser, CSforALL Sarah Heckman, North Carolina State University Bella Gransbury White, North Carolina State University |
Meeting Room E146 |
| Thursday, 1:45-3pm PT | Unlocking Excellence in Educational Research: Guidelines for High-Quality Research that Promotes Learning for All | Monica McGill (IACE), Sarah Heckman (North Carolina State University), Michael Liut (University of Toronto Mississauga), Ismaila Temitayo Sanusi (University of Eastern Finland), Claudia Szabo (The University of Adelaide) | Portland Ballroom 252 |
| Thursday, 3:45-5pm PT | The NSF Project Showcase: Building High-Quality K-12 CS Education Research Across an Outcome Framework of Equitable Capacity, Access, Participation, and Experience | Monica McGill (IACE) | Meeting Rooms E143-144 |
| Friday, 10am PT | The Landscape of Disability-Related K-12 Computing Education Research (poster) | Julie Smith (IACE), Monica McGill (IACE) | Exhibit Hall E |
| Friday, 10:45am PT | Piloting a Diagnostic Tool to Measure AP CS Principles Teachers’ Knowledge Against CSTA Teacher Standard 1 | Monica McGill (IACE), Joseph Tise (IACE), Adrienne Decker (University at Buffalo) | Meeting Room D136 |
| Saturday, 10am PT | Reimagining CS Courses for High School Students (poster) | Julie Smith (IACE), Bryan Twarek (CSTA), Monica McGill (IACE) | Exhibit Hall E |
To learn more about SIGCSE, click the link below.
Key Levers for Advancing K-12 Computer Science Education
Comments Off on Key Levers for Advancing K-12 Computer Science EducationComputer science has become an essential skill for K-12 students. As the demand for computing jobs grows, there is a pressing need to advance K-12 CS education across the nation. To achieve this, there are several key levers that can advance change, including policy changes, teacher training and development, increased access to technology and resources, and partnerships between educational institutions, non-profits, and industry leaders. By leveraging these, we can equip students with the skills they need to thrive in an increasingly digital world and drive innovation and progress.
Under funding and direction from the CME Group Foundation, we took a look at K-12 computer science education in Chicago and Illinois, in context with efforts across the United States. As a result of this work, we are pleased to announce our most recent publication on this work, Key Levers for Advancing K-12 CS Education in Chicago, in Illinois and in the United States.
In particular, the Foundation funded this study to understand:
- How the landscape of K-12 CS education in Chicago has changed across 2013- 2022, with a focus on public schools, out-of-school-time (OST) programs, and research for evidence of progress.
- The current strengths and opportunities of the K-12 CS education landscape in Chicago, in Illinois, and nationally.
- How the support from the Foundation since it first started funding K-12 CS education in Chicago in 2015 has influenced the CS education landscape.
This qualitative study, conducted by Laycee Thigpen, Annamaria Lu, Monica McGill (all from the Institute for Advancing Computing Education), and Eva Giglio (CME Group Foundation), involved conducting 49 interviews (57 people in total). The interviewees represented a wide variety of organizations and voices.
Key findings for Chicago Public Schools (CPS) include the need to:
- Support consistency and fidelity across schools
- Continue to address the teacher shortage and to support the need for teacher CS professional development
- Support research within CPS to inform decision-making to improve equitable outcomes for all students
- Support workforce pathways for high school students
- Support expanded K-8 CS, including integration into other subject areas
- Support the design of scaffolded, standards-based curriculum
Specific to out-of-school time programs, we found that there is a need to support the creation, implementation and maintenance of ways to search CS learning opportunities and for program providers to also engage in partnerships with schools.
The report also details more findings for Illinois–some of which are similar, others that differ to meet the unique needs of rural communities.
We look forward to hearing your thoughts on the report!
