Demystifying Reliability and Validity in Educational Research

Posted by Monica McGill on | Comments Off on Demystifying Reliability and Validity in Educational Research

Post prepared and written by Joe Tise, PhD, Senior Education Researcher

In the past, reliability and validity may have been explained to you by way of an analogy: validity refers to how close to the “bullseye” you can get on a dart board, while reliability is how consistently you throw your darts in the same spot (see figure below).

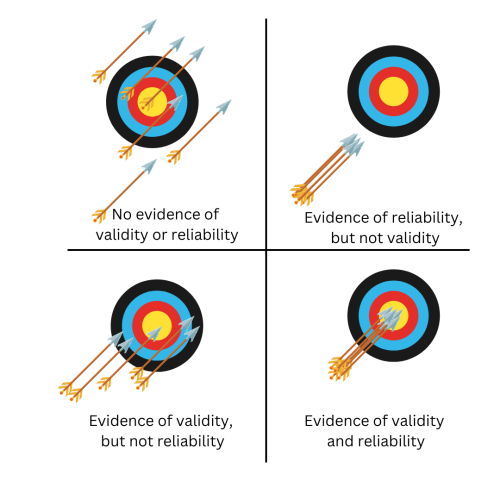
Four images of arrows and targets to represent when reliability and validity can be achieved.

Such an analogy is largely useful, but somewhat reductive. In this four-part blog series, I will dig a bit deeper into validity and reliability to show the different types of each, the different conceptualizations of each, and the relations between them. The structure and content in this blog post comes largely from the Standards for Educational and Psychological Testing (2014), so I highly recommend you get a copy of that book to learn more.

Validity

The Standards (American Educational Research Association et al., 2014) define validity as “the degree to which evidence and theory support the interpretations of test scores for proposed uses of tests.” This definition leads me to make an important distinction at the outset: a test is never valid or invalid—it is the interpretations and uses of that test and decisions made because of a test that are valid or invalid.

To illustrate this point, consider the following scenario. I want to measure students’ reading fluency. I dig into a big pile of data I collected from thousands of K12 students and see that taller students can read longer and more complex books than shorter students. I say to myself:
“Great! To assess new students’ reading fluency, all I need to do is measure how tall they are. Taller students are better readers, after all. Thus, a measure of students’ height must be a valid test of reading fluency.”

Of course, you likely see a problem with my logic. Height may well be correlated with reading fluency (because older children tend to be taller and better readers than younger children), but clearly it is not a test of reading fluency. Nobody would argue that my measuring tape is invalid—just that my use of it to measure reading fluency is invalid. This distinction, obvious as it may seem, is the crux of contemporary conceptions of validity (American Educational Research Association et al., 2014; Kane, 2013). Thus, researchers ought never say a test is valid or invalid but rather, their interpretations or uses of a test are valid or invalid. We may, however, say that an instrument has evidence of validity and reliability while bearing in mind the relevance of such evidence may apply differentially among populations, settings, points in time, or other factors.

Reliability

A similar distinction must be made about reliability—reliability refers to the data, rather than the test itself. A test that produces reliable data will produce the same result for the same participants after multiple administrations, assuming no change in the construct has occurred (e.g., assuming one did not learn more about math between two administrations of the same math test). Thus, The Standards define reliability as “the more general notion of consistency of the scores across instances of the testing procedure.”

But how can you quantify such consistency in the data across testing events? Statisticians have several ways to do this, each differing slightly depending on their theoretical approach to assessment. Each approach utilizes some form of a reliability coefficient, or “the correlation between scores on two equivalent forms of the test, presuming that taking one form has no effect on performance on the second form.” There are many theories of assessment, but three of the most common include Classical Test Theory (Gulliksen, 1950; Guttman, 1945; Kuder & Richardson, 1937), Generalizability Theory (Cronbach et al., 1972; Suen & Lei, 2007; Vispoel et al., 2018) and Item Response Theory (IRT) (Baker, 2001; Hambleton et al., 1991). This blog post is too broad in scope to detail each of these theories, but just know that each theory differs in assumptions made about assessment, terminology used, and each has different implications for how one quantifies data reliability.

What’s Next?

This post only introduces these two terms. The next three posts discuss validity and reliability more in-depth for both quantitative and qualitative approaches (to be published over the next few weeks).

References
American Educational Research Association, American Psychological Association, & National Council on Measurement in Education. (2014). Standards for Educational and Psychological Testing. American Educational Research Association.

Baker, F. B. (2001). The Basics of Item Response Theory (2nd ed.). ERIC Clearinghouse on Assessment and Evaluation. https://eric.ed.gov/?id=ED458219

Cronbach, L. J., Gleser, G. C., Nanda, H., & Rajaratnam, N. (1972). The dependability of behavioral measurements: Theory of generalizability for scores and profiles. John Wiley and Sons.

Gulliksen, H. (1950). Theory of Mental Tests. Wiley.

Guttman, L. (1945). A basis for analyzing test-retest reliability. Psychometrika, 10(4), 255–282. https://doi.org/10.1007/BF02288892

Hambleton, R. K., Swaminathan, H., & Rogers, H. J. (1991). Fundamentals of Item Response Theory. Sage Publications, Inc.

Kane, M. (2013). The argument-based approach to validation. School Psychology Review, 42(4), 448–457. https://doi.org/10.1080/02796015.2013.12087465

Kuder, G. F., & Richardson, M. W. (1937). The theory of the estimation of test reliability. Psychometrika, 2(3), 151–160. https://doi.org/10.1007/BF02288391
Suen, H. K., & Lei, P.-W. (2007). Classical versus Generalizability theory of measurement. Educational Measurement, 4, 1–13.

Vispoel, W. P., Morris, C. A., & Kilinc, M. (2018). Applications of generalizability theory and their relations to classical test theory and structural equation modeling. Psychological Methods, 23(1), 1–26. https://doi.org/10.1037/met0000107

Comments are closed